The Typed Transformer: Intro and architecture
Or, dependently typed Python
We walk through a tutorial implementation of an encoder-decoder transformer model in JAX. We focus on types to: bring clarity to the implementation, and demonstrate Python typing techniques.
Contents
Intro
There1 are already a number of introductions to the basic transformer architecture used in language models:
- The original paper introducing the architecture: Attention is All You Need
- The Annotated Transformer
- And the excellent Illustrated Transformer
But those are all for normal people who have a healthy and pragmatic relationship with programming. Perhaps, like me, you had Haskell sidle up to you in a fragile moment and offer you a vision of a shining future in which all your code possessed a pure and timeless beauty.
Why a typed transformer?
This2 vision may consume you. And once it does, you may find yourself claiming that a typed transformer implementation:3
- Makes the fuzzy and implicit precise and explicit. For example, I had code that I had written before the availability of variadic generics in Python. When I went back to add variadic generics, I realized that I had not even properly understood my own code!
- Greatly reduces the strain on sharpy limited working memory. Mentally tracking all the dimensions in even mildly complex code is impossible so many ML codebases contain an ad hoc, informally-specified, bug-ridden, non-checkable set of comments annotating the dimensions of tensors. See the figure below for one example.
- Tightens the feedback loop. This is especially valuable for ML code where, without a type checker, you may wait for your data to load and JAX to compile only to find out that you made a trivial mistake. With my current typing discipline, I essentially never have runtime issues of this sort. My errors only reflect my fundamental ignorance and comprehensive conceptual confusion rather than my carelessness.
- Demonstrates that Python’s typing facilities are pretty okay and let you encode some useful invariants.
def forward(self, prev_hidden, batch_H, char_onehots):
# [batch_size x num_encoder_step x num_channel] -> [batch_size x num_encoder_step x hidden_size]
batch_H_proj = self.i2h(batch_H)
prev_hidden_proj = self.h2h(prev_hidden[0]).unsqueeze(1)
e = self.score(torch.tanh(batch_H_proj + prev_hidden_proj)) # batch_size x num_encoder_step * 1
alpha = F.softmax(e, dim=1)
context = torch.bmm(alpha.permute(0, 2, 1), batch_H).squeeze(1) # batch_size x num_channel
concat_context = torch.cat([context, char_onehots], 1) # batch_size x (num_channel + num_embedding)
cur_hidden = self.rnn(concat_context, prev_hidden)
return cur_hidden, alphaThe plan
Thus4 we work through an implementation of a basic transformer in Python using Python’s optional typing facilities5. The hope is that (as the first point above suggests) well-chosen types are an effective pedagogical tool to minimize the ambiguity that characterizes novice learning. (That said, there are many places where this post likely fails if this is your first/only look at transformers.)
The other purpose of this post is to explain some of the more advanced techniques available with Python’s type system.
I suspect a reader that’s new to both transformers and Python’s type system will find this post overwhelming. So really, there are two alternative readings for this post: one that explains some type tricks to ML people and one that introduces transformers to the terminally type-brained. If you’re already comfortable with Python’s type system, you can perhaps skip directly to the crux—the typed implementation of attention.
A repository containing all this code and a training loop for a basic seq2seq task is available here.
The Typed Transformer
Transformers6 are, of course, used for sequence to sequence tasks. That is, it’s an architecture suitable for use with a variable length collection of inputs that produces a variable length collection of outputs. Famously, this includes natural language text.
Python typing preliminaries
We’ll first introduce some Python typing tools that we’ll use throughout the model.
One7 crucial tool is the Fin type:
class Fin[Int: int](int):
def __new__(x: int | ndarray[int], max_: Int) -> Fin[Int]:
assert 0 <= x < max_
return cast(Any, x)There are a few things to note here:
class Fin[Int: int](int): ...uses the new type parameter syntax to express thatFinis a generic type parameterized by a type calledInt. ThatIntis constrained to be a subtype ofint.- Our
Intsubtype will always be an integer literal type. An integer literal type is a type that corresponds to some particular integer value likeLiteral[10]. - A type of
Fin[Int](short for finite set) conveys that the value it corresponds to is in the range[0, Int). For example, 0, 1, and 2 are the valid values of typeFin[Literal[3]]. See Haskell’sfinpackage for reference. Finonly exists in the type system. At runtime, our values are just ordinaryints. This is directly analogous toNewType, butNewTypedoes not support type parameters.- We will be using this type to represent the relationship between the size of our model’s vocabulary and the tokens in that vocabulary. Using a single type variable (e.g.
Vocab) to represent both would be inaccurate but using two distinct variables would fail to encode all the information we know about these concepts.Fin[VocabSize]perfectly captures the relationship by expressing that the allowable token values depend on the vocabulary size.
With this in hand, we can describe a sequence of token IDs used for input as:
This8 is a type alias declaration and also our first look at variadic generics. Our numpy type stub declares the type of numpy.ndarray as class ndarray[*Shape, DType]. DType works in the straightforward, expected way (i.e. it declares what type (float32, int64, etc) each element of the array is) while *Shape expresses that ndarray accepts a variable number of type arguments beyond DType. In this case, the number of additional arguments corresponds to the number of dimensions in the array and each argument expresses the size of the corresponding dimension9. So ndarray[SeqLen, Fin[VocabSize]] is a 1D array (i.e. vector) of length SeqLen where each element is a token from our vocabulary. And ndarray[SeqLen, EmbedDim, Float] would be a 2D array (i.e. matrix) where we have SeqLen rows, each of which has an EmbedDim width.
Architecture overview
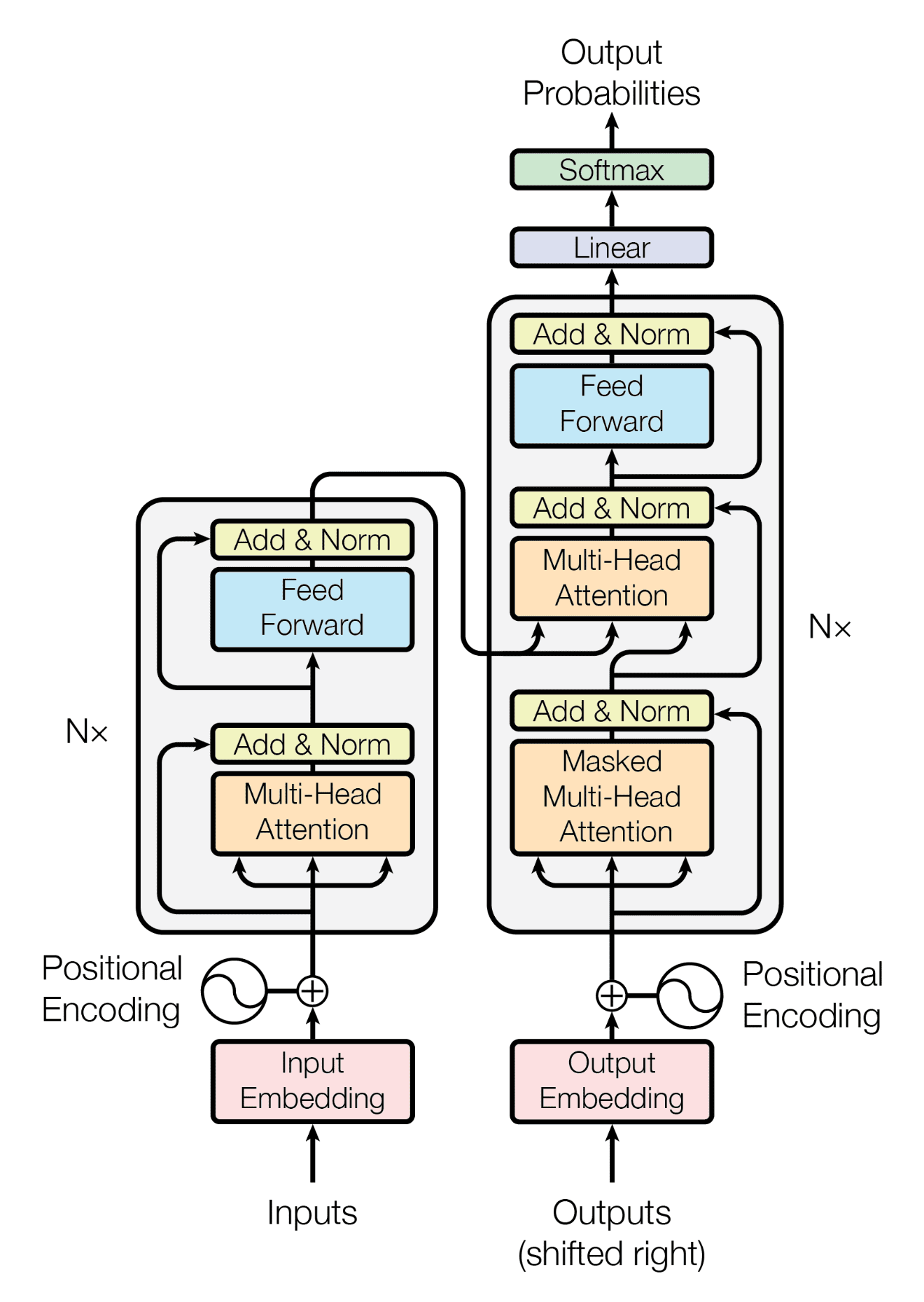
Now that we’ve introduced our most essential typing primitives, we can jump into a walk through of our simple transformer. We implement the architecture depicted10 in this diagram:
Embedder
We11 start with the embedder block—responsible for transforming the sequence of token IDs in the input into a sequence of embedding vectors:
class Embedder[VocabSize: int, MaxSeqLen: int, EmbedDim: int, Float: float](eqx.Module):
token_embedder: eqx.nn.Embedding[VocabSize, EmbedDim, Float]
position_embedder: eqx.nn.Embedding[MaxSeqLen, EmbedDim, Float]
norm: eqx.nn.LayerNorm[EmbedDim, Float]
def __init__(
self,
*,
vocab_size: VocabSize,
max_seq_len: MaxSeqLen,
embed_size: EmbedDim,
key: KeyArray,
):
...
def __call__[SeqLen: int](
self, token_ids: ndarray[SeqLen, Fin[VocabSize]]
) -> ndarray[SeqLen, EmbedDim, Float]:
tokens: ndarray[SeqLen, EmbedDim, Float] = jax.vmap(self.token_embedder.__call__)(token_ids)
assert token_ids.shape[0] <= self.position_embedder.num_embeddings
positions: ndarray[SeqLen, EmbedDim, Float] = jax.vmap(self.position_embedder.__call__)(
# jnp.arange(SeqLen) produces `ndarray[SeqLen, Fin[SeqLen]]`
# (i.e. a 1D array of length `SeqLen` where
# each element is a value in the range [0, SeqLen))
# Our `assert` guarantees we can safely cast this to `Fin[MaxSeqLen]`
declare_dtype[Fin[MaxSeqLen]](jnp.arange(token_ids.shape[-1]))
)
return jax.vmap(self.norm.__call__)(tokens + positions)This is our first Equinox module so here are some notes:
VocabSize,MaxSeqLen,EmbedDimandFloatare declared as type parameters for the class. We use type parameters like this for values that are both: fixed at instance creation time (i.e. any particular instance ofEmbedderwill only work with a single embedding dimensionality, etc); and are externally visible (i.e. they affect how this module may or may not fit together with other modules).SeqLenon the other hand is a type parameter that can vary from__call__to__call__—subject to the constraint that it’s less thanMaxSeqLen.- The distinct purposes of the two embedders can immediately be read off from the types—one projects tokens (
Fin[VocabSize]) into embedding vectors (EmbedDim) and the other projects positions (Fin[MaxSeqLen]) into embedding vectors. - Note that we use absolute position embedding for simplicity but other position embedding schemes are typical for real models. Some sort of position embedding is essential because the attention mechanism fundamentally views its input as a set of unordered elements.
- I’ve explicitly written in the types for declarations like
tokensandpositionsfor pedagogical purposes, but these can be omitted and inferred by the type checker. - Note how few degrees of freedom we have. This
__call__is pretty trivial and so not prone to mistakes, but there are many bad implementations which are simply impossible to write with this type signature. vmapstands for “vectorizing map”. It lifts a function to operate on an additional axis of an array. In this case, we use it to apply embedders that work token-wise to each element in the sequence.- (We explicitly invoke
__call__because it makes jump-to-definition functionality work better in (at least some) editors.)
Multi-head attention
As12 we trace through our architecture diagram, we see that the next stop is the heart of the transformer: multi-head attention. This is where contextual understanding across sequence elements is built up. It’s also the most complicated part of the transformer and, I claim, the part where types bring the most additional clarity.
We13 start with a helper function that computes attention for a particular head when given queries, keys and values. We’ll discuss a somewhat inefficient implementation here that makes the semantics obvious. The proper implementation is shown in an appendix:
def dot_product_attention_for_query[QKDim: int, KVSeqLen: int, VDim: int, Float: float](
query: ndarray[QKDim, Float], keys: ndarray[KVSeqLen, QKDim, Float], values: ndarray[KVSeqLen, VDim, Float]
) -> ndarray[VDim, Float]:
query = query / jnp.sqrt(query.shape[-1]).astype(query.dtype)
logits: ndarray[KVSeqLen, Float] = jax.vmap(ft.partial(jnp.dot, query))(keys)
weights: ndarray[KVSeqLen, Float] = jax.nn.softmax(logits)
return jnp.average(values, axis=0, weights=weights)
def vmap_dot_product_attention[QSeqLen: int, QKDim: int, KVSeqLen: int, VDim: int, Float: float](
queries: ndarray[QSeqLen, QKDim, Float],
keys: ndarray[KVSeqLen, QKDim, Float],
values: ndarray[KVSeqLen, VDim, Float],
) -> ndarray[QSeqLen, VDim, Float]:
def inner(query: ndarray[QKDim, Float]) -> ndarray[VDim, Float]:
return dot_product_attention_for_query(query, keys, values)
return jax.vmap(inner)(queries)We can read off from the types that:
- We can have a different number of sequence elements for the queries and keys and values.
- The key and query must be compatible in their embedding dimensionality but the value can be different. It’s the value embedding dimensionality that determines the output dimensionality.
Semantically, we are doing a dot product between each key and query vector. If the vectors are all of similar magnitude, the dot product will measure the cosine similarity between the vectors. Thus each query will have more weight assigned to keys that are more similar in this sense. softmax normalizes these weights so that the the attention allocated across all keys for a given query sums to 1.
(We also omit masking in this toy implementation. The essence of masking is just that masked positions are given logits of negative infinity so that they get no weight and don’t affect the output. See the actual implementation in the appendix.)
Now14 that we’ve gotten the helper out of the way, we’ll look at multi-head attention itself. We’ll take it in two pieces:
# In `numpy` type stub
class Product[*Shape](int): ...
# In user code
def product_[*Shape](operands: tuple[*Shape]) -> Product[*Shape]:
"""Retain type info when computing the product of a tuple."""
return cast(Any, prod(cast(tuple[int, ...], operands)))
class MHAttention[QDim: int, KDim: int, VDim: int, OutputDim: int, Float: float](eqx.Module):
# Purely internal types that shouldn't be visible to callers
type _NumHeads = InstanceSingleton[Literal["NumHeads"]]
type _QKSize = InstanceSingleton[Literal["QKSize"]]
type _VOSize = InstanceSingleton[Literal["VOSize"]]
query_proj: eqx.nn.Linear[QDim, Product[_NumHeads, _QKSize], Float]
key_proj: eqx.nn.Linear[KDim, Product[_NumHeads, _QKSize], Float]
value_proj: eqx.nn.Linear[VDim, Product[_NumHeads, _VOSize], Float]
output_proj: eqx.nn.Linear[Product[_NumHeads, _VOSize], OutputDim, Float]
num_heads: _NumHeads = eqx.field(static=True)Productis another one of our type helpers. It allows us to represent the result of a multiplication in a semantically useful way.- We have projection matrices for each of the query, key, value and output. Because it’s multi-head attention, each projection matrix turns a single
QDimquery vector into vector with a length ofNumHeads * QKSize(and similarly for the other projection matrices). This is what theProductsignifies vs a head-by-head projection which would involveeqx.nn.Linear[QDim, _QKSize, Float]projection matrices. - The type parameters here remind us that
MHAttentionusers need to be aware of the query, key, value and output dimensionality for the particularMHAttentioninstance at hand. - However, the number of heads, the QK size and the VO size are internal details that aren’t mechanically relevant to other modules. We signify this with
InstanceSingletonwhich acts as a sort of private type variable (actually declaring a private type variable doesn’t work in Pyright). - Here, I think types have decisively paid off. Holding all 8–12 (depending on how you count) of these parameters active in working memory is only possible if you’ve already committed them to long-term memory.
And15 here’s the full multi-head attention computation:
def _project[InDim: int, SeqLen: int, OutDim: int](
self,
proj: eqx.nn.Linear[InDim, Product[MHAttention._NumHeads, OutDim], Float],
x: ndarray[SeqLen, InDim, Float],
) -> ndarray[SeqLen, MHAttention._NumHeads, OutDim, Float]:
projection: ndarray[SeqLen, Product[MHAttention._NumHeads, OutDim], Float] = jax.vmap(proj)(x)
return jnp.reshape(projection, (x.shape[0], self.num_heads, cast(OutDim, -1)))
def __call__[QSeqLen: int, KVSeqLen: int](
self,
query: ndarray[QSeqLen, QDim, Float],
key_: ndarray[KVSeqLen, KDim, Float],
value: ndarray[KVSeqLen, VDim, Float],
mask: ndarray[QSeqLen, KVSeqLen, bool] | None = None,
) -> ndarray[QSeqLen, OutputDim, Float]:
query_heads: ndarray[QSeqLen, MHAttention._NumHeads, MHAttention._QKSize, Float] = self._project(
self.query_proj, query
)
key_heads: ndarray[KVSeqLen, MHAttention._NumHeads, MHAttention._QKSize, Float] = self._project(
self.key_proj, key_
)
value_heads: ndarray[KVSeqLen, MHAttention._NumHeads, MHAttention._VOSize, Float] = self._project(
self.value_proj, value
)
attn: ndarray[QSeqLen, MHAttention._NumHeads, MHAttention._VOSize, Float] = jax.vmap(
ft.partial(dot_product_attention, mask=mask), in_axes=1, out_axes=1
)(query_heads, key_heads, value_heads)
concatenated_attention: ndarray[
QSeqLen, Product[MHAttention._NumHeads, MHAttention._VOSize], Float
] = jnp.reshape(attn, (query.shape[0], product_(attn.shape[1:])))
return jax.vmap(self.output_proj)(concatenated_attention)_projectis a helper which, given a projection matrix and a sequence, projects each sequence element and then splits the output by head. (The projection matrices are combined across heads with the output being split after matmul for efficiency.)- We use that helper to produce sequences with query, key and value projections for each head.
- We
vmapover the heads to independently capture multiple aspects of the input sequence. The result is that each head produces aQSeqLensequence ofVOSizedimensionality embeddings. - Then we concatenate the sequences again before transforming our
VOSizeembeddings intoOutputDimembeddings with the final projection matrix. - Again, I think the types are quite helpful here. There are several moving pieces and they’re being reshaped back and forth for performance reasons. Tracking them with types is much more reliable than tracking them mentally and the resulting typed code is almost trivial.
And that’s it! That’s the kernel at the heart of the recent wave of generative AI.
Masking
But there are, of course, many other parts of the architecture that we need for a complete model.
Next16 up in our diagram and in the flow of data through the model is the self-attention layer. But first we take a brief detour to discuss masking—a mechanism for making certain sequence elements “invisible” to attention:
# fmt: off
@dataclass(frozen=True)
class NoMask: pass # noqa: E701
@dataclass(frozen=True)
class CausalMask: pass # noqa: E701
type MaskType = NoMask | CausalMask
# fmt: on
def mk_mask[SeqLen: int](
padding_mask: ndarray[SeqLen, bool], *, mask_type: MaskType
) -> ndarray[SeqLen, SeqLen, bool]:
full_padding_mask: ndarray[SeqLen, SeqLen, bool] = jnp.expand_dims(padding_mask, axis=-1) * jnp.expand_dims(
padding_mask, axis=-2
)
match mask_type:
case NoMask():
return full_padding_mask
case CausalMask():
causal_mask = jnp.tril(jnp.ones((padding_mask.shape[0], padding_mask.shape[0]), bool), k=0)
return full_padding_mask * causal_mask- We encode algebraic data types (the other kind of ADT) as a union (sum) of
dataclasses (products) (though they’re empty products in this case). - Note that there are really two distinct kinds of masking happening in transformers:
- Causal masking: Causal masking—only used in the decoder half—reflects the semantic demands of our training setup17. For efficiency reasons, we present the decoder with the whole target sequence at once. Without causal masking, the decoder could “cheat” by looking at future tokens and trivially achieve perfect performance at the training task in a way that’s entirely useless. Causal masking ensures that the decoder actually learns deeper structural features of the data by making “future” tokens invisible at each “time step”. See the figure below for an illustration.
- Padding masking: Even though our input sequences may have different lengths, we need each sequence in a batch to have the same length. Thus, shorter sequences are padded out with a special padding token. Padding masking effectively makes these padding tokens invisible to attention so that spurious correlations aren’t learned.
mk_masktakes a padding mask and a causal masking type and “interprets” them to produce a full square mask suitable for direct use with the attention mechanism.

Self-attention
And18 now self-attention itself which builds a contextual understanding of a singular sequence:
class SelfAttention[EmbedDim: int, Float: float](eqx.Module):
attention: MHAttention[EmbedDim, EmbedDim, EmbedDim, EmbedDim, Float]
norm: eqx.nn.LayerNorm[EmbedDim, Float]
mask_type: MaskType = eqx.field(static=True)
def __init__(self, *, embed_dim: EmbedDim, num_heads: int, mask_type: MaskType, key: KeyArray):
self.attention = MHAttention(num_heads=num_heads, query_size=embed_dim, key=key)
self.norm = eqx.nn.LayerNorm(shape=embed_dim)
self.mask_type = mask_type
def __call__[SeqLen: int](
self, input_: ndarray[SeqLen, EmbedDim, Float], padding_mask: ndarray[SeqLen, bool]
) -> ndarray[SeqLen, EmbedDim, Float]:
mask: ndarray[SeqLen, SeqLen, bool] = mk_mask(padding_mask, mask_type=self.mask_type)
attn_out: ndarray[SeqLen, EmbedDim, Float] = self.attention.__call__(
query=input_, key_=input_, value=input_, mask=mask
)
return jax.vmap(self.norm.__call__)(attn_out + input_)- The self-attention layer is just a multi-head attention layer where the query, key, value and output dimensionality are all the same.
- Correspondingly, the input sequence is used as the query, key and value. This might seem slightly strange or silly—what good is it to pretend the same value is three distinct things?—but the projection matrices learn to extract different features of the input sequence.
- When self-attention is used in the encoder, the
mask_type19 will beNoMaskbecause we expect the encoder to have access to the full input sequence. In the decoder’s self-attention, we’ll useCausalMaskduring training to ensure that the model learns behavior that generalizes to inference—where future tokens won’t be available.
Feed forward
The20 final building block before we can look at the whole encoder layer is a simple feed forward block:
class FeedForward[EmbedDim: int, Float: float](eqx.Module):
type _HiddenDim = InstanceSingleton[Literal["HiddenSize"]]
hidden: eqx.nn.Linear[EmbedDim, _HiddenDim, Float]
output: eqx.nn.Linear[_HiddenDim, EmbedDim, Float]
norm: eqx.nn.LayerNorm[EmbedDim, Float]
...
def __call__(self, input_: ndarray[EmbedDim, Float]) -> ndarray[EmbedDim, Float]:
output: ndarray[EmbedDim, Float] = self.output.__call__(
jax.nn.gelu(self.hidden.__call__(input_)),
)
return self.norm.__call__(output + input_)- As we’ve discussed,
_HiddenDimusesInstanceSingletonto signal that, while_HiddenDimis some particular value which the two linear layers need to be compatible on, it’s not a value that’s directly relevant for other modules. - We use
geluas the activation function but note that other choices are possible too. Similarly,RMSNormhas become a popular alternative toLayerNorm. - The activation function in the feed forward block is the key non-linearity in the transformer. The composition of any number of linear operations is itself linear so we could only learn linear functions without this non-linearity.
- Note that, throughout our architecture, we use a “post-LN” convention. This is simply to conform with most of the introductory material but the position of layer normalization has substantial impacts on gradient flow. In my limited tests, sprinkling layer norms everywhere as described in the NormFormer paper is substantially more effective than either pre-LN or post-LN.
Encoder block
Now21 that we’ve described most of our building blocks and type machinery, we can pick up the pace. An encoder block is composed of a self-attention layer followed by a feed forward layer:
class EncoderLayer[EmbedDim: int, Float: float](eqx.Module):
self_attention: SelfAttention[EmbedDim, Float]
feed_forward: FeedForward[EmbedDim, Float]
...
def __call__[SeqLen: int](
self, input_: ndarray[SeqLen, EmbedDim, Float], mask: ndarray[SeqLen, bool]
) -> ndarray[SeqLen, EmbedDim, Float]:
attn_out: ndarray[SeqLen, EmbedDim, Float] = self.self_attention.__call__(input_, mask)
return jax.vmap(self.feed_forward.__call__)(attn_out)- Each encoder layer has an opportunity to both build up contextual understandings by letting different pieces of the input sequence “communicate” via self-attention and to elaborate those understandings on an independent basis via a
vmap-ed feed forward layer. - Note that, as both the self-attention and feed forward layers add the input back at the end (
attn_out + input_andoutput + input_), the whole encoder layer effectively retains a residual connection. This means that, during the forward pass, these layers only have to worry about learning to extract useful signals rather than learning to extract useful signals in an information-preserving way. And it helps manage the vanishing gradient problem during the backward pass.
Encoder stack
An22 encoder stack is just a sequence of encoder layers which lets the encoder progressively develop more sophisticated understandings of the input sequence:
class Encoder[EmbedDim: int, Float: float](eqx.Module):
layers: tuple[EncoderLayer[EmbedDim, Float], ...]
...
def __call__[SeqLen: int](
self, embeds: ndarray[SeqLen, EmbedDim, Float], padding_mask: ndarray[SeqLen, bool]
) -> ndarray[SeqLen, EmbedDim, Float]:
for layer in self.layers:
embeds = layer.__call__(embeds, padding_mask)
return embeds- Note that, for non-tutorial implementations, you’d want to JAX’s
scanfunctionality (as described here or here) instead of Python loop. With a Python loop, JAX will compile N distinct copies of the layer which greatly increases compilation time and memory usage. Unfortunately, not every implementation does this.
Encoder
And23 finally, the encoder first has to transform the tokens into initial embeddings before passing them through the stack:
class EmbeddingEncoder[VocabSize: int, MaxSeqLen: int, EmbedDim: int, Float: float](eqx.Module):
embedder: Embedder[VocabSize, MaxSeqLen, EmbedDim, Float]
encoder: Encoder[EmbedDim, Float]
pad_token_id: Fin[VocabSize] = eqx.field(static=True)
...
def __call__[SeqLen: int](
self, token_ids: ndarray[SeqLen, Fin[VocabSize]]
) -> ndarray[SeqLen, EmbedDim, Float]:
embeds: ndarray[SeqLen, EmbedDim, Float] = self.embedder.__call__(token_ids)
return self.encoder.__call__(embeds, token_ids != self.pad_token_id)- As we can read off from the types, the input to the
EmbeddingEncoderis a sequence of token IDs. The sequence lengthSeqLenis at mostMaxSeqLenand each token ID is in the range[0, VocabSize). The output is a sequence of the same length as the input but each element is now anEmbedDimdimensional embedding representing the contextual semantics of the corresponding token in high dimensional space. - The split between
EncoderandEmbeddingEncoderis a bit gratuitous for the present use case, but we sometimes want to use an encoder as a generic way to process a sequence and this split decouples that task from the specifics of tokenization and embedding.
Cross-attention
We24 have now covered the encoder half of the architecture. But we are more than halfway done because the only new build block in the decoder half is cross-attention. Where self-attention used the same sequence for each of the query, key and value, cross-attention uses the encoder output sequence for keys and values and the decoder’s input sequence for queries. In other words, cross-attention allows the decoder to interpret the decoder input sequence in the context of the encoder sequence.
class CrossAttention[QDim: int, KVDim: int, Float: float](eqx.Module):
attention: MHAttention[QDim, KVDim, KVDim, QDim, Float]
norm: eqx.nn.LayerNorm[QDim, Float]
...
def __call__[QSeqLen: int, KVSeqLen: int](
self,
query: ndarray[QSeqLen, QDim, Float],
key_value: ndarray[KVSeqLen, KVDim, Float],
query_padding_mask: ndarray[QSeqLen, bool],
key_value_padding_mask: ndarray[KVSeqLen, bool],
) -> ndarray[QSeqLen, QDim, Float]:
attn_out: ndarray[QSeqLen, QDim, Float] = self.attention.__call__(
query=query,
key_=key_value,
value=key_value,
mask=jnp.expand_dims(query_padding_mask, axis=-1) * jnp.expand_dims(key_value_padding_mask, axis=-2),
)
return jax.vmap(self.norm.__call__)(attn_out + query)- Note how the query dimensionality (
QDim) of the decoder input sequence is slotted into theQDimandOutputDimpositions in theMHAttentiontype parameters while the key and value dimensionality (KVDim) of the encoder output sequence is slotted into theKDimandVDimpositions. - Note also that we have two distinct sequence lengths—one corresponding to the decoder input sequence (
QSeqLen) and one corresponding to the encoder sequence (KVSeqLen). - Finally, note that we simply directly construct the attention mask from the padding mask—there’s no causal masking as the decoder is allowed to look at the full encoder output sequence. (And note that our types ensure that we don’t mix up the mask dimensions.)
Decoder block
A25 decoder block is like an encoder block but with an additional cross-attention layer so the decoder can attend to the encoder output:
class DecoderLayer[QDim: int, KVDim: int, Float: float](eqx.Module):
self_attention: SelfAttention[QDim, Float]
cross_attention: CrossAttention[QDim, KVDim, Float]
feed_forward: FeedForward[QDim, Float]
...
def __call__[QSeqLen: int, KVSeqLen: int](
self,
query: ndarray[QSeqLen, QDim, Float],
key_value: ndarray[KVSeqLen, KVDim, Float],
query_padding_mask: ndarray[QSeqLen, bool],
key_value_padding_mask: ndarray[KVSeqLen, bool],
) -> ndarray[QSeqLen, QDim, Float]:
self_attn_out: ndarray[QSeqLen, QDim, Float] = self.self_attention.__call__(query, query_padding_mask)
cross_attn_out: ndarray[QSeqLen, QDim, Float] = self.cross_attention.__call__(
query=self_attn_out,
key_value=key_value,
query_padding_mask=query_padding_mask,
key_value_padding_mask=key_value_padding_mask,
)
return jax.vmap(self.feed_forward.__call__)(cross_attn_out)Everything here should be pretty unsurprising at this point.
Decoder stack
The26 decoder is just a sequence of decoder layers:
class Decoder[QDim: int, KVDim: int, Float: float](eqx.Module):
layers: tuple[DecoderLayer[QDim, KVDim, Float], ...]
...
def __call__[OutSeqLen: int, InSeqLen: int](
self,
query: ndarray[OutSeqLen, QDim, Float],
key_value: ndarray[InSeqLen, KVDim, Float],
query_padding_mask: ndarray[OutSeqLen, bool],
key_value_padding_mask: ndarray[InSeqLen, bool],
) -> ndarray[OutSeqLen, QDim, Float]:
for layer in self.layers:
query = layer.__call__(query, key_value, query_padding_mask, key_value_padding_mask)
return queryThe only thing to note is the brief reminder about the value of—in a real implementation—using scan instead of a Python loop.
Decoder
And27 the decoder which again combines the token embedding and contextual understanding tasks:
class EmbeddingDecoder[VocabSize: int, MaxSeqLen: int, EmbedDim: int, Float: float, MaskT: MaskType](eqx.Module):
embedder: Embedder[VocabSize, MaxSeqLen, EmbedDim, Float]
decoder: Decoder[EmbedDim, EmbedDim, Float]
pad_token_id: Fin[VocabSize] = eqx.field(static=True)
...
def __call__[OutSeqLen: int, InSeqLen: int](
self,
query: ndarray[OutSeqLen, Fin[VocabSize]],
key_value: ndarray[InSeqLen, EmbedDim, Float],
key_value_padding_mask: ndarray[InSeqLen, bool],
) -> ndarray[OutSeqLen, EmbedDim, Float]:
embeds: ndarray[OutSeqLen, EmbedDim, Float] = self.embedder.__call__(query)
return self.decoder.__call__(embeds, key_value, (query != self.pad_token_id), key_value_padding_mask)We’ve now described both halves of the model.
Encoder-decoder transformer
So28 we can finally put them together into a full encoder-decoder transformer:
class Output[*Shape, InSeqLen, OutSeqLen, EmbedDim, VocabSize, Float](NamedTuple):
encoder_output: ndarray[*Shape, InSeqLen, EmbedDim, Float]
decoder_output: ndarray[*Shape, OutSeqLen, EmbedDim, Float]
logit_output: ndarray[*Shape, OutSeqLen, VocabSize, Float]
class LM[EmbedDim: int, VocabSize: int, MaxSeqLen: int, Float: float](eqx.Module):
encoder: EmbeddingEncoder[VocabSize, MaxSeqLen, EmbedDim, Float]
decoder: EmbeddingDecoder[VocabSize, MaxSeqLen, EmbedDim, Float, CausalMask]
logit: eqx.nn.Linear[EmbedDim, VocabSize, Float]
pad_token_id: Fin[VocabSize] = eqx.field(static=True)
...
def __call__[InSeqLen: int, OutSeqLen: int](
self,
encoder_ids: ndarray[InSeqLen, Fin[VocabSize]],
decoder_ids: ndarray[OutSeqLen, Fin[VocabSize]],
*,
mask_type: MaskType,
) -> Output[InSeqLen, OutSeqLen, EmbedDim, VocabSize, Float]:
enc_out: ndarray[InSeqLen, EmbedDim, Float] = self.encoder.__call__(encoder_ids)
decoder_out: ndarray[OutSeqLen, EmbedDim, Float] = self.decoder.__call__(
decoder_ids, enc_out, (encoder_ids != self.pad_token_id)
)
logits: ndarray[OutSeqLen, VocabSize, Float] = jax.vmap(self.logit.__call__)(decoder_out)
return Output(enc_out, decoder_out, logits)- The
*Shapetype parameter onOutputallows us to reuse the same type declaration for single batch elements (with*Shapeas an empty sequence) as we do here, for a whole batch of many outputs (with*ShapeasBatchLen), and potentially for batches sharded across devices (with*Shapeas(NumDevices, BatchLen)). - We process the input sequence via the encoder and then use that output as keys and values for the decoder’s cross-attention.
- The
logitlayer transforms the embedding vectors from the decoder—which are an abstract semantic representation—into logits over the vocabulary. This lets us generate actual token IDs as output by e.g. taking the argmax of the logits.
Outro
And there you have it. We have laid out a well-typed implementation of the fundamental architecture for a transformer-based model. While relatively straightforward, this architecture is enough to learn highly sophisticated language modeling behavior at scale. To briefly recap:
- We take a sequence of discrete inputs in the form of tokens. We represent each token as
Fin[VocabSize]whereVocabSizeis the number of possible tokens. - We embed these tokens into a high-dimensional space via an
Embedder. Each embedding vector is anndarray[EmbedDim, Float]. - On the encoder side, we use a stack of
EncoderLayers to build up a contextual understanding of the embedded input sequence. - The key to this contextual understanding is
MHAttention.MHAttentionuses learned projection matrices to extract relevant features from a sequence of query, key and value embeddings. Each projected query is then compared to all projected keys to determine the weight to allocate across projected values. - In
SelfAttention, the query, key and value are all the same sequence soMHAttentionlearns how each part of the sequence influences the interpretation of other parts. FeedForwardlayers work on attention output on an element-wise basis and introduce essential non-linearity.- On the decoder side, we use a stack of
DecoderLayers to built up a contextual understanding of the decoder input sequence in the context of the encoder sequence. - In particular,
CrossAttentionuses the encoder output as keys and values and the decoder input as queries so thatMHAttentionlearns how each part of the encoder output influences the interpretation of each part of the decoder input. - Once the decoder has built up a final semantic representation in embedding space, a logit layer transforms these embeddings into concrete logits over the vocabulary.
Throughout, we focused on the careful use of types (especially variadic generics on our tensors) to reduce ambiguity and succinctly convey essential information about the contract fulfilled by each piece of functionality.
While this architecture is useful for a variety of tasks, we still haven’t actually embedded it in a particular task and training context. We will demonstrate what that looks like in a future post.
Appendix
Performance-oriented dot product attention
In the explanation above, we used a tutorial implementation of dot product attention that very directly reflects the semantics. However, quick microbenchmarks suggest that it takes ~10x longer to run than the conventional implementation:
def dot_product_attention_weights[QSeqLen: int, QKDim: int, KSeqLen: int, Float: float](
query: ndarray[QSeqLen, QKDim, Float],
key: ndarray[KSeqLen, QKDim, Float],
mask: ndarray[QSeqLen, KSeqLen, bool] | None = None,
) -> ndarray[QSeqLen, KSeqLen, Float]:
query = query / jnp.sqrt(query.shape[-1]).astype(query.dtype)
logits: ndarray[QSeqLen, KSeqLen, Float] = query @ key.T
if mask is not None:
logits = jnp.where(mask, logits, jnp.array(jnp.finfo(logits.dtype).min))
return jax.nn.softmax(logits, axis=-1)
def dot_product_attention[QSeqLen: int, QKDim: int, KVSeqLen: int, VDim: int, Float: float](
query: ndarray[QSeqLen, QKDim, Float],
key_: ndarray[KVSeqLen, QKDim, Float],
value: ndarray[KVSeqLen, VDim, Float],
mask: ndarray[QSeqLen, KVSeqLen, bool] | None = None,
) -> ndarray[QSeqLen, VDim, Float]:
weights: ndarray[QSeqLen, KVSeqLen, Float] = dot_product_attention_weights(query, key_, mask)
return weights @ valueThe difference is just that, instead of doing the attention on vmaped per-query basis, we use highly optimized matrix multiplication routines to handle the whole set of queries simultaneously.
A nearly, dearly departed darling
I think this technique is pretty cute but probably not worthwhile in 99.9% of Python code bases; I removed it, but I couldn’t quite bear to part with it entirely:
class LTE[A: int, B: int](int):
"""A refinement type on `A` that witnesses that `A <= B`.
Or, from another view, it's a `Fin` in which we don't discard the input type
but retain info about both values passed to the constructor.
`LTE[Literal[2], Literal[3]]` is simply a `2` with additional evidence that `2 <= 3`.
`LTE[Literal[4], Literal[3]]` OTOH is uninhabitable
(i.e. any attempt to construct such a value would raise an assertion error).
"""
def __new__(cls, a: A, b: B) -> LTE[A, B]:
assert a <= b
return cast(Any, a)
class Embedder[VocabSize: int, MaxSeqLen: int, EmbedDim: int, Float: float](eqx.Module):
token_embedder: eqx.nn.Embedding[VocabSize, EmbedDim, Float]
position_embedder: eqx.nn.Embedding[MaxSeqLen, EmbedDim, Float]
norm: eqx.nn.LayerNorm[EmbedDim, Float]
...
def __call__[SeqLen: int](
self, token_ids: ndarray[LTE[SeqLen, MaxSeqLen], Fin[VocabSize]]
) -> ndarray[LTE[SeqLen, MaxSeqLen], EmbedDim, Float]:
tokens: ndarray[LTE[SeqLen, MaxSeqLen], EmbedDim, Float] = jax.vmap(self.token_embedder.__call__)(
token_ids
)
positions: ndarray[LTE[SeqLen, MaxSeqLen], EmbedDim, Float] = jax.vmap(self.position_embedder.__call__)(
# jnp.arange(LTE[SeqLen, MaxSeqLen]) produces
# `ndarray[LTE[SeqLen, MaxSeqLen], Fin[LTE[SeqLen, MaxSeqLen]]]`
# By the definition of `LTE`, `Fin[LTE[SeqLen, MaxSeqLen]]` can be safely cast to `Fin[MaxSeqLen]`
declare_dtype[Fin[MaxSeqLen]](jnp.arange(token_ids.shape[-1]))
)
return jax.vmap(self.norm.__call__)(tokens + positions)The main thing we do here is, instead of asserting that SeqLen <= MaxSeqLen at runtime, we require a type-level witness of this constraint. The underlying philosophy here is that it’s better to push requirements “upstream” than to pass failures “downstream”. But we introduce a non-negligible amount of extra machinery (that’s pretty foreign to the average Pythonista) for what’s a pretty marginal benefit here. This sort of technique might be justifiable if we had a more complex and pervasive set of interlocking requirements with a higher cost of failure.
There are multiple extant intros you should read.↩︎
Types can be particularly useful for ML code.↩︎
I’m not trying to mount an exhaustive defense of static typing here—just highlighting the benefits most relevant for this par have ticular context.↩︎
The post serves two purposes: explaining transformers for the type-brained and types for the transformer-brained.↩︎
In particular, I use Pyright. I can’t say for certain how other type checkers will handle this code.↩︎
Transformers are seq2seq models.↩︎
Finis a useful type for describing vocabularies and tokens.↩︎Variadic generics allow us to describe ND tensors.↩︎
The PEP itself acknowledges some uncertainty about what semantics we should assign to array dimensions. Should they merely label the “kind” of dimension it is (batch, channel, etc) or the precise size of the dimension? IMO the convention I’ve settled on makes a number of useful type-level properties possible to express with minimal drawbacks.↩︎
Both images in this post are lifted from The Annotated Transformer.↩︎
The embedder block transforms a sequence of tokens IDs into a sequence of embedding vectors.↩︎
Multi-head attention is where contextual understanding is established.↩︎
We compute attention for a sequence of queries, keys and values.↩︎
Types help us track all the projection matrix dimensions in mult-head attention.↩︎
Types also help us track reshaping across attention heads.↩︎
We have two distinct types of masking: padding and causal masking.↩︎
At inference time, the causal mask is not strictly necessary. “Cheating” is impossible during auto-regressive token generation. But a causal mask ensures: we can reuse cached decoder states during generation; and that our inference matches the training task—the decoder has no training experience on how to handle future tokens.↩︎
Self-attention is used to build up a contextual understanding of a single sequence.↩︎
Many implementations pass a
maskargument to__call__which implicitly embeds the decision of whether to causally mask or not. I think our implementaiton—where we regard this causal masking behavior as a fixed at module creation time—is more semantically appropriate and less error-prone. The standard approach implies that we can freely choose to apply causal masking or not at__call__time, but a self-attention block trained with causal masking will not likely generalize to an unmasked setting.↩︎The feed forward block’s most important role is introducing non-linearity.↩︎
The encoder block is composed of a self-attention layer followed by a feed forward layer.↩︎
The encoder stack builds a contextual, semantic representation of a sequence via a succession of encoder blocks.↩︎
The encoder turns a sequence of tokens into a sequence of contextual, semantic embeddings.↩︎
Cross-attention allows the decoder to interpret the decoder input sequence in the context of the encoder sequence.↩︎
A decoder block allows the model to build up a contextual understanding of one sequence in the context of another sequence.↩︎
The decoder stack builds a contextual, semantic representation of one sequence in the context of another via a succession of decoder blocks.↩︎
The decoder turns a sequence of tokens into a sequence of semantic embeddings in the context of another sequence of embeddings.↩︎
An encoder-decoder transformer processes an input sequence via the encoder half and auto-regressively generates output via the decoder.↩︎